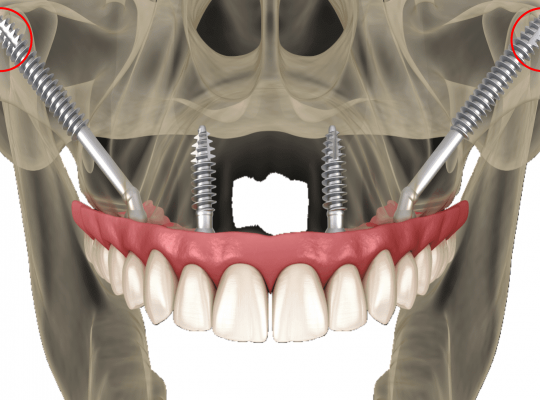
В чем отличие базальной имплантации от обычной?
Имплантация — один из методов решения проблемы утраченных зубов. Важно понимать различия между базальной и традиционной имплантацией, чтобы сделать осознанный выбор в пользу оптимального лечения. Что представляет собой процесс зубной имплантации? Зубная имплантация — процедура замещения потерянных зубов, при которой в челюстную кость вживляется искусственный корень. На него впоследствии ставится зубная коронка. Это позволяет не …